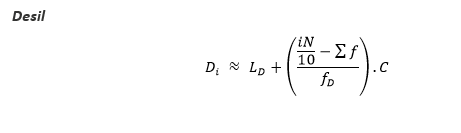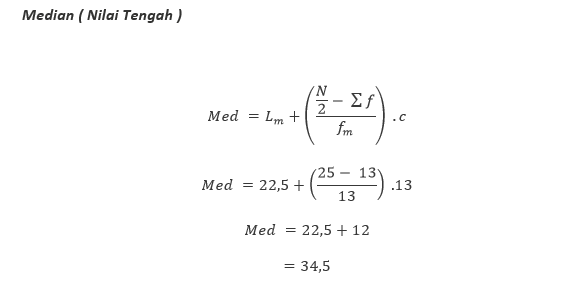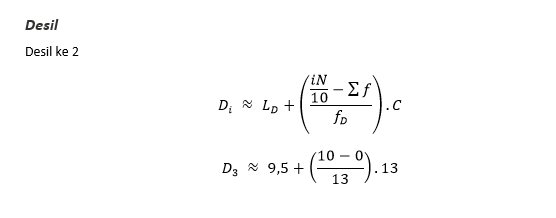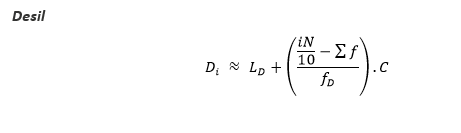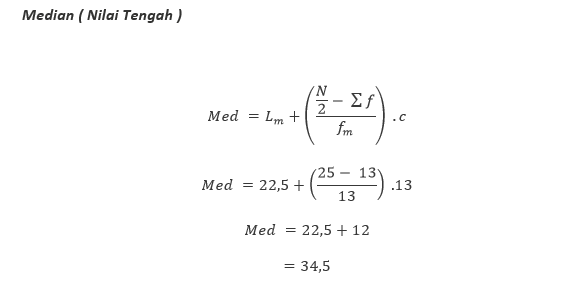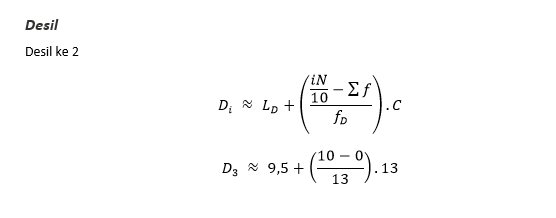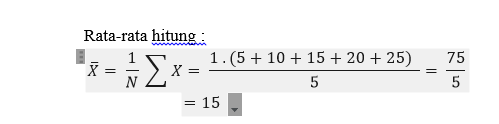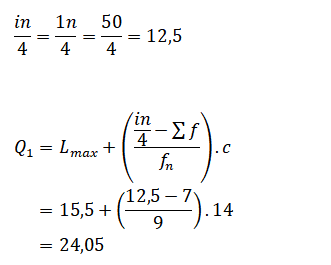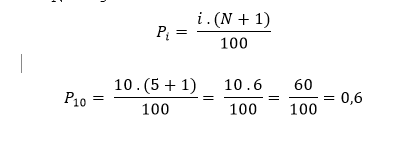Ukuran Gejala Pusat Dikelompokan

Pengertian Data Dikelompokan

 

Data yang dikelompokkan adalah data yang sudah disusun ke dalam sebuah distribusi frekuensi sehingga data tersebut mempunyai interval kelas yang jelas dan mempunyai titik tengah kelas.

Rata – rata hitung (mean)

Median ( Nilai Tengah )

Modus

Kuartil

Desil

Persentil

 

Ukuran Varians dan Simpangan Baku

Pengertian Varians

Varians adalah salah satu ukuran dispersi atau ukuran variasi.  Varians dapat menggambarkan bagaimana berpencarnya suatu data kuantitatif.  Varians diberi simbol  σ² (baca: sigma kuadrat) untuk populasi dan untuk s² sampel. 

Selanjutnya kita akan menggunakan simbol s²  untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.

Rumus untuk menghitung varians ada dua , yaitu rumus teoritis dan rumus  kerja.  Namun demikian, untuk mempersingkat  tulisan ini, maka kita gunakan rumus kerja saja.  Rumus kerja ini mempunyai kelebihan dibandingkan rumus teoritis, yaitu hasilnya lebih akurat dan lebih mudah mengerjakannya.

Pengertian Simpang Baku

Simpangan baku didefinisikan sebagai akar kuadrat varians. Simpangan baku merupakan bilangan tak-negatif, dan memiliki satuan yang sama dengan data. Misalnya jika suatu data diukur dalam satuan meter, maka simpangan baku juga diukur dalam meter pula. Istilah rumus simpangan bakupertama kali diperkenakan oleh Karl Pearson pada tahun 1894, dalam bukunya On the dissection of asymmetrical frequency curves.

Jenis-jenis ukuran variasi:

 

 Jangkauan ( Range )

 

Simpangan Rata-Rata

       Diketahui data = 5,10,15,20,25
       N     = 5

• 

       Simpangan rata-rata =

 

 

Varians dan Simpangan Baku 

 Dik data = 5,10,15,20,25
       N     = 5
Rata-rata hitung :

Maka Varians :

Maka Simpangan Baku :

 

 

Kuartil :

 Kuartil ke-1

Kuartil ke-2

 


 Jangkauan Persentil

  Dik data = 5,10,15,20,25
       N     = 5

P10 = X0 + 0,6 . (X1-X0)
      =0+0,6. (5-0)
      =0+0,6 . (5-0)
      =0+3 = 3

P90 = X5 + 0,4 . (X6-X5)
      =25+0,4. (0-25)
      =25+(-10)
      =15

 

 Referensi: https://hatta2stat.wordpress.com/2011/05/19/varians/

 

Ukuran Gejala Pusat Data Tidak Berkelompok

Ukuran Gejala Pusat Data Belum Dikelompokkan

Ukuran pemusatan data yang termasuk ke dalam analisis statistika deskriptif adalah rata-rata hitung (mean), median, modus, dan fraktil (kuartil, desil, persentil).

Berikut ini adalah macam-macam ukuran gejala pusat data yang sudah di kelompokkan, yaitu:

1.      Rata-Rata Hitung (mean)

Istilah mean dikenal dengan sebutan angak rata-rata. Nilai rata-rata hitung (mean) adalah total dari semua data yang diperoleh dari jumlah seluruh nilai data dibagi dengan jumlah frekuensi yang ada.

            Untuk mencari rata-rata hitung berupa data kelompok, maka terlebih dahulu  harus ditentukan titik tengah dari masing-masing kelas.    

2.      Median

Median merupakan sebuah nilai data yang berada di tengah-tengah dari rangkaian data yang telah tersusun secara teratur. Hasil median sama dengan hasil dari kuartil kedua.

Rumus median : ke (N + 1)/2.

Jika N ganjil : N = 2k + 1 maka Med = X k+1

Jika N genap : N = 2k maka

Med = ½ (X k + X k+1 )

3.      Modus

Modus merupakan nilai data yang memiliki frekuensi terbesar atau nilai data yang paling sering muncul.

Modus ( Sering Muncul / Data frekuensi paling tinggi)

4.      Kuartil

Pada prinsipnya, pengertian kuartil sama dengan median. Perbedaanya hanya terletak pada banyaknya pembagian kelompok data. Median membagi kelompok data atas 2 bagian, sedangkan kuartil membagi kelompok data atas 4 bagian yang sama besar, sehingga akan terdapat 3 kuartil yaitu kuartil ke-1, kuartil ke-2 dan kuartil ke-3, dimana kuartil ke-2 sama dengan median.

5.      Desil

Desil adalah suatu rangkaian data yang membagi suatu distribusi menjadi 10 bagian yang sama besar.

6.      Persentil

            Persentil adalah ukuran letak yang membagi suatu distribusi menjadi 100 bagian yang sama besar.

 

7.      Jangkauan (range)

Jangkauan atau range adalah selisih antara data pengamatan terbesar dengan data pengamatan terkecil yang terdapat pada kumpulan suatu data tersebut.

Rumus jangkauan (range): R=Xmax-Xmin

 

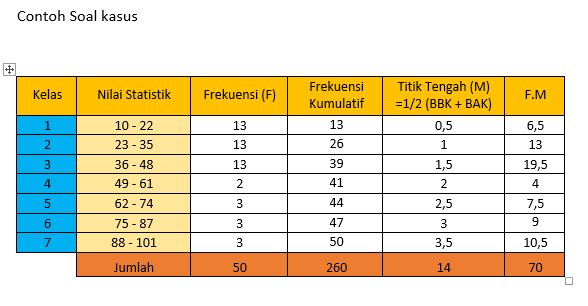
Contoh Perhitungannya:

•           Mean

Diketahu data : X1=5,X2=10,X3=15,X4=20,X5=25

Maka rata-rata hitungnya adalah?

Penyelsaian :

•           Rata-rata ukur

Diketahui data : X1=5,X2=10,X3=15,X4=20,X5=25

Maka rata-rata hitungnya adalah?

Penyelsaian :

 

•           Rata-rata harmonis

Diketahui data : X1=5,X2=10,X3=15

Maka rata-rata hitungnya adalah?

Penyelsaian :

  

•           Rata-rata tertimbang

Diketahui data : Xi =1,2,3   Wi =4,5,6

 

•           Median data ganjil

Diketahui data : 3,5,9          N=3

•           Median data genap

Diketahui data : 3,5,9,11          N=4

 

•           Modus

Diketahui data : X1=2,X2=2,X3=3, X4=4

Modusnya adalah 2

•           Kuartil

Diketahui : 3,4,5,6,7

Q1 ?       N= 5

 

Q1=X1+0,5(X2-X1)

     =3+0,5(4-3)

     =3,5

•           Desil

Diketahui :

3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22

D1 ?       N= 20

D1=X2+0,1(X3-X2)

     =4+0,1(5-4)

     =4,1

•Persentil

Diketahui :

3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,8282,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102

P5 ? N= 100

  P5=X5+0,50(X6-X5)

     =7+0,50(8-7)

     =7,5

 

Contoh membuat descriptive statics:

 

Klik datapada tab data->lalu pilih data analysis maka akan muncul seperti ini:

 

Lalu pilih  dexcriptive statics:

Pilih input range->lalu klik data yang ingin di input ke input range:

 

           Pilih/ceklis label in first row->ceklis summary statics->klik ok->finish

 

Maka akan jadi seperti ini:

 

 

 REFERENCE:

https://www.blogger.com/blogger.g?blogID=5052599477984194653#editor/target=post;postID=7939407135337836955 

http://belajarpintar-id.blogspot.com/2018/02/makalah-ukuran-gejala-pusat-data-belum.html